このページでは「オームの法則」の計算を中学生向けに詳しく説明するよ。
また、このページは中二理科の電気の単元の５ページ目
なんだ。
電流・電圧・抵抗の基本を理解せずに、オームの法則だけを勉強しても問題は解けるようにならないよ。
時間があるときには１から学習してみてね☆
全てのページを読むと電気の学習が完璧になるよ。
ぜひチャレンジしてみてね！
中学生におすすめ勉強アプリ
「Rakumon（ラクモン）」というアプリを知っていますか？
チャットや画像を送るだけで質問ができるアプリです。10分で答えや解説が返ってきますよ。
３回は無料で使えるので、登録しておくと役立ちますよ！
ラクモンの説明はこちら
このページの内容は、私が書いた下の本でさらに詳しく学習できます！
とてもわかりやすいので、ぜひご利用くださいね！
それではオームの法則の学習スタートです！
オームの法則とは
では「オームの法則」の学習を始めよう。
ねこ吉オームの法則って、よく聞くけど、どんな法則なの？
難しい言い方をすると、オームの法則とは、「電流の大きさは電圧に比例し、抵抗に反比例する」
という法則なんだよ。
ねこ吉確かに難しい…
難しい言い方をするとね。
だから簡単で便利な覚え方をするといいよ。
オームの法則とは、
「電流・電圧・抵抗のうち、２つがわかると残りの１つがわかる」
という法則なんだよ。
ねこ吉２つがわかると残りの１つがわかる？
そう覚えるといいよ。
公式を使いながら確かめていこう。
オームの法則の公式
では公式の説明をするよ。
２つあるけど、②の公式がおすすめだよ。
①普通の公式
②便利な公式
記号で覚えると→
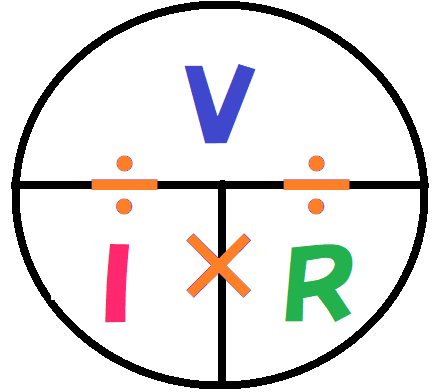
言葉で覚えたければ左、記号で覚えたければ右で覚えてね！
ねこ吉先生、②の便利な公式って、どうやって使うんだっけ？
では公式も使いながら、オームの法則の便利さを説明していくね☆
例１ 抵抗を知りたい場合
始めに話をした通り、オームの法則は
「電流・電圧・抵抗のうち、２つがわかると残りの１つがわかる」という法則だったね。
例１では電流、電圧がわかって、
抵抗を知りたい場合の問題を解いてみよう！
例１ 抵抗を求めよ。
電流が２Ａ、電圧が10Ｖ、２つがわかっているから、抵抗を求められるね。
（Ｒというのは抵抗がわからないときに使う記号だよ。）
便利な公式を使うよ。
この公式は「知りたいものを隠す」ようにして使うんだ。
この場合は抵抗を知りたいから、抵抗を隠そう。
そうすると、電圧、電流が縦に並んで残るね。
縦に残った場合は「上÷下」つまり
電圧÷電流をすると抵抗がわかるんだ。
（電圧と電流の間の÷の所にある黒の線を分数の横線と考えて、「電流分の電圧」と考えてもいいよ☆）
つまり、１０÷２＝５ となって
答えは 抵抗は５Ω となるね。
ねこ吉電流と電圧がわかれば、オームの法則で抵抗がわかるんだね！
例２ 電流を知りたい場合
次は電流を知りたい場合の問題だよ。
例２ 電流を求めよ。
電圧が５Ｖ、抵抗が20Ω。２つがわかっているから、電流を求められるね。
（Ｉ（アイ）というのは電流がわからないときに使う記号だよ。）
便利な公式を使うよ。
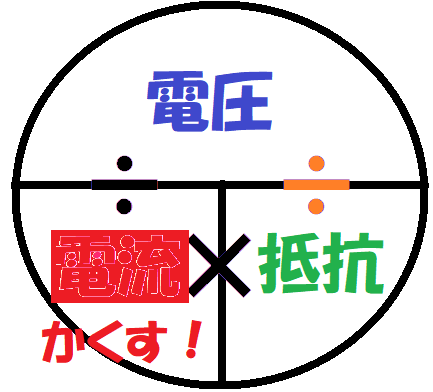
今回は電流を知りたいから、電流を隠そう。
そうすると、電圧、抵抗が縦に並んで残るね。
縦に残った場合は「上÷下」つまり
電圧÷抵抗をすると電流がわかるんだ。
（電圧と電流の間の÷の所にある黒の線を分数の横線と考えて、「抵抗分の電圧」と考えてもいいよ☆）
つまり、５÷20＝0.25 となって
答えは 電流は0.25A となるね。
ねこ吉抵抗と電圧がわかれば、オームの法則で電流がわかるんだね！
例３ 電圧を知りたい場合
次は電圧を知りたい場合の問題だよ。
例３ 電圧を求めよ。
電流が500mA、抵抗が30Ω。２つがわかっているから、電圧を求められるね。
（Vというのは電流がわからないときに使う記号だよ。）
便利な公式を使うよ。
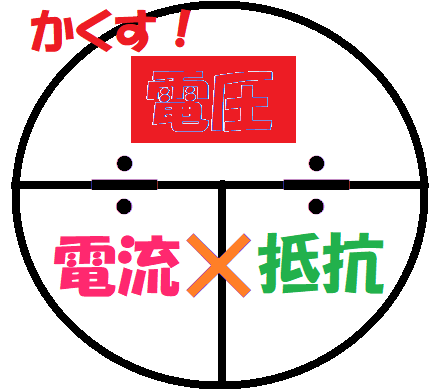
今回は電圧を知りたいから、電圧を隠そう。
そうすると、電流、抵抗が横に並んで残るね。横に残った場合は「左×右」つまり
電流×抵抗をすると電圧がわかるんだ。
（オームの法則を使うときは、電流の単位は必ずmA→Aになおすよ）
つまり、0.5×30＝15 となって
答えは 電圧は１５Ｖ となるね。
ねこ吉抵抗と電圧がわかれば、オームの法則で電流がわかるんだね！
オームの法則を使った計算
オームの法則の公式と基本はわかったかな？
ねこ吉うん。オームの法則は電流、電圧、抵抗のうち、２つがわかると残りの１つがわかる法則だね！
その通り！
では少し難しい問題を解いてみよう。
回路の問題は慣れることが大切だからね！
直列回路
直列回路からチャレンジしよう。
問１-① 上の回路の回路全体の抵抗はいくらか。
問１-② 電流計に流れる電流はいくらか。
問１-③ 12Ωの抵抗にかかる電圧はいくらか。
（解き方を考えてみてね！）
考えたかな？それでは
問１-① 上の回路の回路全体の抵抗はいくらか。
から解いていこう。
ねこ吉はどう考えた？
ねこ吉ええっと、オームの法則を使って…
それは間違いなんだよ。注意してね！
え、そうなの？
そうなんだ。オームの法則を覚えると、すぐ使いたくなるよね。
けど、オームの法則の前に、電流・電圧・抵抗の基本知識で答えが出ないか？
と考えるようにしよう！
（基本知識がわからない人は、下のボタンから、①～④のページを読んできてね！）
もう一度、問１-①をみるよ。
この回路の「回路全体の抵抗」を出せばいいんだよね？
どうする？
ねこ吉あ、前のページでやった、直列回路の全体抵抗の出し方。「足し算するだけ」だ！
そう！
直列回路の回路全体の抵抗の出し方は足すだけだね！
答えは６+１２＝18Ωだね！
次は問１-② 電流計に流れる電流はいくらか。
だね。
ここでは、「回路全体の電圧」「回路全体の抵抗」がわかっているから、
「オームの法則」で回路全体の電流が出せるよ！
抵抗は「回路全体の抵抗（18Ω）」として考えることがポイントだよ！
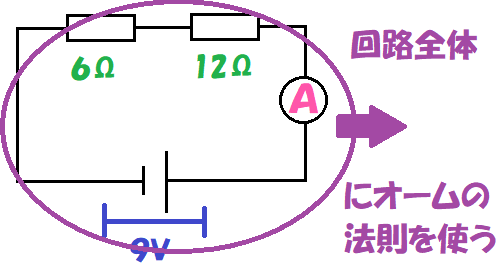
ではオームの法則を使おう。
つまり、９÷18＝0.5 となって
答えは 電流は0.5A となるね。
最後は問１-③ 12Ωの抵抗にかかる電圧はいくらか。
だね。
この「V」にかかる電圧を求めればいいんだね。
これは、オームの法則を「12Ω」の所に使うよ！
もう一つポイントは、
「直列回路だから、回路のどの部分にも0.5Aの電流が流れている」
ということだね！
もちろん、12Ωのところにも0.5Aの電流が流れているからオームの法則は
つまり、0.5×12＝６ となって
答えは 電圧は6V となるね。
イメージ図でもこの回路を見てみよう！
こんな感じだね！このイメージ図が浮かぶ人はかなりレベルUPしてるよ☆
おまけだけど、ねこ吉は６Ωの抵抗にかかる電圧を求める方法が２つ思い浮かぶ？
ねこ吉２つ？
そう。1つ目は、問１-③と同じようにオームの法則を使う方法だね。
すると
0.5×６＝３ となって
答えは 電圧は３V となるね。
もう一つは、「電圧がよくわかる４つのルール」を使う方法だね。
４つのルールはここから
① 電源（電池）電池②では電圧の高さが上がる。（必ず電源の＋側が高くなる。）
② 電球電球と抵抗抵抗では電圧の高さが下がる。
③ 導線は高さが変化しない（長さに関係なく）
④ 回路を1周したとき、高さは「０」である。
これを使えば、9V上がって、6V下がっているから、あとは3V下がれば0に戻るとわかるね。
答え 電圧は３V
ねこ吉ほんとだ！オームの法則でも電圧の4つのルールでも同じ答えになるね！
そう。「2つの考え方で同じ答えになる」ところまでわかってくると、「回路が得意」と言ってもいいね☆
並列回路
次は並列回路にチャレンジしよう。
問２-① 上の回路の回路全体の抵抗はいくらか。
問２-② 電圧計が示す電圧はいくらか。
問２-③ 12Ωの抵抗に流れる電流はいくらか。
（解き方を考えてみてね！）
では問２の①からだね。
並列回路の回路全体の抵抗を求める公式
が思い出せるかな？
２つあるけど、①
1 R全体 = 1 R1 + 1 R2 + 1 R3か②
R全体 = R1 × R 2 R1 ＋ R 2のどちらかが思い出せればいいね！
それでは計算しよう。
①の公式でやるね。
（両方覚えた人は②のほうが計算が楽だよ）
1 R全体 = 1 R1 + 1 R2 + 1 R3今回は抵抗が２つでＲ3はいらないね。
1 R全体 = 1 12 + 1 6右辺を通分して
1 R全体 = 1 12 + 2 12右辺を足して
1 R全体 = 3 12右辺を約分して
1 R全体 = 1 4ここで終わりにしないでね
方程式の左辺と右辺は、同時に分子と分母を逆にしてもいいというルールがあるから、両辺の分子と分母を入れ替えよう。
R全体＝４
答えは4Ωだね。
次に問２の②電圧計が示す電圧はいくらか。だね。
回路全体に流れる電流が0.6A、
回路全体の抵抗が4Ω
とわかったから、回路全体にオームの法則を使うよ。
つまり、0.6×４＝2.4 となって
答えは 電圧は2.4V となるね。
最後に問２-③ 12Ωの抵抗に流れる電流はいくらか。だね
イメージ図ものせるね。
つまり、12Ωの抵抗にかかる電圧（イメージ図の高さの変化）は9Vだよね。
12Ωの抵抗の所にオームの法則を使うよ。
すると
2.4÷12＝0.2 となって
0.2Aが答えだね。
ねこ吉。おまけだけど、
6Ωの抵抗の流れる電流を求める方法。２つわかるかな？
ねこ吉わかるよ！１つめはオームの法則を使う方法。
ねこ吉もう一つは、0.6Aのうち、0.2Aが12Ω側に行ってるから、6Ω側は残りの0.4Aが流れているという考え方だね！
その通り。どちらも0.4Aが答えとなるね！
すばらしい☆
さて、これでオームの法則の解説を終わるよ。
ここまで読んだ人はそれだけですごい！
ぜひ自分で自分をほめてあげよう！
これでひとまず回路の学習を終わるけど、「①～⑤」の記事は必ず何度も何度も読んでね。
電流の勉強を続けたい人は⑥の記事も読んでみてね！
さわにいは、登録者６万人のYouTuberです。
中学の成績を上げたい人は、ぜひYouTubeも見てみてね！
また、2022年10月に学習参考書も出版しました。よろしくお願いします。
他のページも見たい人はトップページへどうぞ。
中学生におすすめ勉強アプリ
「Rakumon（ラクモン）」というアプリを知っていますか？
チャットや画像を送るだけで質問ができるアプリです。10分で答えや解説が返ってきますよ。
３回は無料で使えるので、登録しておくと役立ちます！
ラクモンの詳しい説明はこちら
Rakumon（ラクモン）
無料
ねこ吉またねー！
コメント
コメント一覧 （4件）
勉強させてもらってます。とても分かりやすいのでこれからもお世話になりたいと思っています。
例3が電圧を求めるところ、電流を求めているので訂正された方がよろしいかと。
コロナの中、さわにぃさんのサイトが子どもたちの学習にどんどん役立てばいいですね。
しまさんこんにちは、
ご指摘の通り記事に誤りがあり、修正させていただきました。
励ましのお言葉ありがとうございます。
これからも中学生の役にたてるようがんばります。
今後も何かありましたら、いつでもコメントいただければと思います。
ご迷惑おかけし、申し訳ございませんでした。
ご指摘、ありがとうございました。
コロナに気をつけ、素敵な毎日をお過ごしください！
40代になって趣味で電子工作をはじめようと思い、電気の基礎を勉強できるサイトを探しておりました。
大変興味深く読ませていただき、大変参考になりました。
ありがとうございます。
一つだけ気になったところがありまして、
「最後に問２-③ 12Ωの抵抗に流れる電流はいくらか。だね」
のイメージ図に９Vの記載がありますが、例題では2.4Vになっておりましたので訂正が必要かと思いました。
問題内容であればこちらの思い違いですのでご放念いただければと思います。
これからも役に立つサイトの運営、応援しております。
コメントありがとうございます。
ご指摘の通り誤りがありました。
修正させていただきました。
今後もご指導ご鞭撻、何卒よろしくお願い申し上げます。
匿名様のますますのご活躍を祈っております！